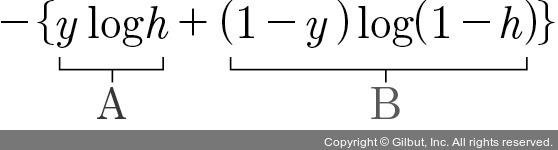아무것도 모르는 공대생의 지식 탐험기
모두의 딥러닝 4일차 (Ch06) 본문
로지스틱 회귀 모델 : 참 거짓 판단하기
로지스틱 회귀(Logistic Regression) 이해하기
머신러닝에서 데이터가 특정 범주에 속하는지를 예측하는 분류(Classification) 문제를 해결하기 위해 로지스틱 회귀(Logistic Regression)가 사용된다. 로지스틱 회귀는 선형 회귀와 유사하지만, 결과를 0과 1 사이의 확률 값으로 변환하는 것이 특징이다. ( 직선이 아닌 참(1)과 거짓(0) 사이를 구분하는 S자 형태의 선을 그어 주는 작업이다)
1. 로지스틱 회귀란?
로지스틱 회귀는 이진 분류(Binary Classification) 문제를 해결하는 데 사용되는 머신러닝 알고리즘이다. 주어진 입력 데이터를 기반으로 특정 데이터가 어느 그룹(클래스)에 속하는지를 예측하는 역할을 한다.
로지스틱 회귀가 활용되는 예시
- 이메일이 스팸인지 아닌지 분류
- 환자가 질병에 걸렸는지 아닌지 예측
- 고객이 상품을 구매할지 여부 예측
시그모이드 함수(Sigmoid Function)를 통해 선형 모델을 확률 값으로 변환할 수 있다.
2. 시그모이드 함수(Sigmoid Function)와 로지스틱 회귀
시그모이드 함수는 입력값을 0과 1 사이의 확률 값으로 변환하는 역할을 한다.
S다 형태의 그래프이다
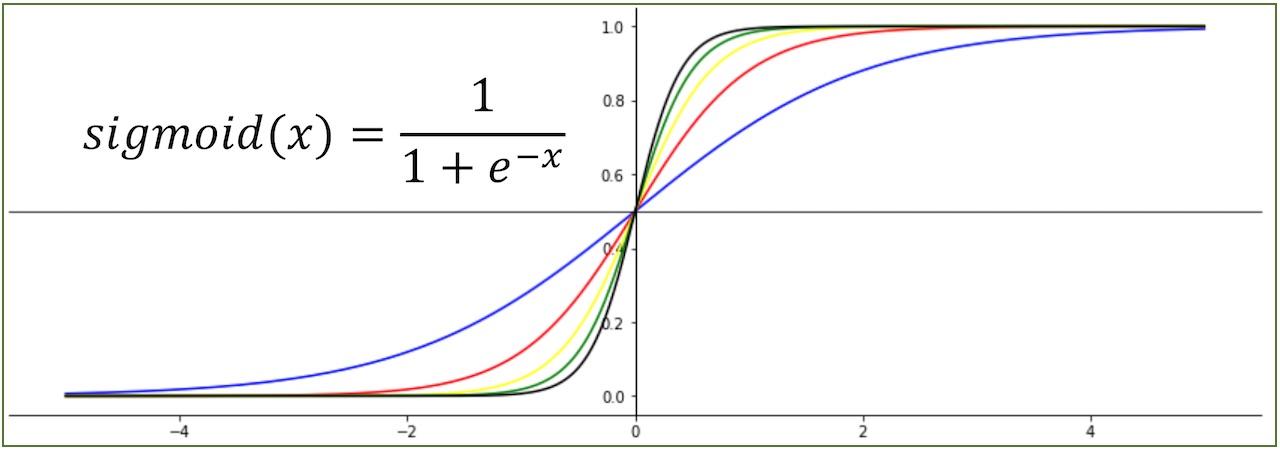
시그모이드 함수의 특징
- 입력 값이 무한대로 커질수록 출력 값은 1에 가까워진다.
- 입력 값이 무한대로 작아질수록 출력 값은 0에 가까워진다.
- 출력 값은 항상 0과 1 사이의 확률 값이다.

- a : 그래프의 경사도
: a값이 커지면 경사가 커지고 a값이 작아지면 경사가 작아짐
: a가 작아질수록 오차는 무한대로 커지지만, a가 커진다고 해서 오차가 없어지지는 않음
- b : 그래프의 좌우 이동
: b값이 크면 왼쪽으로 이동하고 b값이 작아지면 오른쪽으로 이동
: b값이 너무 크거나 작을 경우, 오차는 이차 함수 그래프와 유사한 형태로 나타남
이 특성을 활용하면 데이터를 분류하는 문제를 확률적인 관점에서 해결할 수 있다.
3. 로지스틱 회귀에서 오차 계산 (교차 엔트로피 손실 함수)
로지스틱 회귀는 단순한 선형 회귀와 달리 오차(손실 함수)를 계산할 때 교차 엔트로피 손실 함수(Cross Entropy Loss)를 사용한다.
결국 a와 b를 구하는 것은 돌고 돌아 경사하강법을 사용해야 한다.
- x가 1일때는 y는 0이 되고, x가 0에 가까워질수록 y의 값은 점점 작아짐
- 예측이 타겟과 일치할 때 최소값을 갖고, 예측이 타겟과 다를수록 값이 증가
4. 로그 함수
실제 값이 1인 경우 -log(x)를 사용하며, 0일 때는 -log(1-x)의 그래프를 사용해야 한다.
이는 아래와 같은 방법으로 해결가능하다. (x자리에 h를 대입하면 동일하다.) y에 실제 값을 대입하여 사용한다.
이를 통해 실제값에 따라 빨간색 그래프와 파란색 그래프를 적절히 선택하여 사용가능하다.