아무것도 모르는 공대생의 지식 탐험기
모두의 딥러닝 3일차 (Ch05) 본문
선형 회귀 모델 : 먼저 긋고 수정하기
1. 기울기와 오차의 관계
회귀 분석에서 직선의 방정식은 다음과 같다.
여기서 a(기울기)와 b(절편)을 찾는 것이 핵심이다. 하지만 어떤 값이 최적의 기울기와 절편인지 어떻게 결정할 수 있을까?
기울기와 오차 사이의 관계를 보면 오차는 이차 함수 형태를 띤다. 즉, 기울기가 너무 크거나 너무 작으면 오차가 증가하고, 특정 기울기에서 오차가 최소가 된다.
따라서 오차가 가장 작은 최적의 기울기(m)를 찾아야 한다. 이를 위해 경사 하강법을 활용한다.
2. 경사 하강법(Gradient Descent)이란?
경사 하강법은 오차를 줄이기 위해 기울기를 조정하는 최적화 알고리즘이다. 이 방법은 오차의 변화를 기반으로 적절한 학습률(learning rate)을 설정하고, 점진적으로 최적의 기울기와 절편을 찾아간다.
경사 하강법의 작동 방식
- 임의의 기울기 a1에서 시작하여 오차를 미분해 기울기를 구한다.
- 미분값이 양수면 음의 방향, 음수면 양의 방향으로 이동하며 a2에서 다시 미분을 구한다.
- 미분값이 0이 될 때까지 이 과정을 반복하며 최적의 기울기를 찾아간다.
학습률(learning rate)의 중요성
경사 하강법에서 학습률은 기울기를 조정하는 속도를 결정하는 중요한 요소이다. 학습률이 너무 크면 최적의 기울기에 수렴하지 않고 발산할 수 있으며, 반대로 너무 작으면 학습 속도가 느려진다.
3. 평균제곱오차(MSE)와 경사 하강법을 적용한 단순 선형 회귀
단순 선형 회귀 모델을 경사 하강법을 이용하여 직접 구현해보자.
1) 환경 및 데이터 준비
import numpy as np
import matplotlib.pyplot as plt
x = np.array([2, 4, 6, 8]) # 공부한 시간
y = np.array([81, 93, 91, 97]) # 성적2) 변수 설정
a = 0 # 초기 기울기
b = 0 # 초기 절편
lr = 0.03 # 학습률
epochs = 1701 # 반복 횟수3) 경사 하강법 실행
n = len(x) # 데이터 개수
for i in range(epochs):
y_pred = a * x + b # 예측 값 계산
error = y - y_pred # 실제 값과의 차이 계산
# 편미분을 통해 기울기와 절편 조정
a_diff = -(2/n) * sum(x * error)
b_diff = -(2/n) * sum(error)
# 학습률을 반영하여 기울기와 절편 업데이트
a -= lr * a_diff
b -= lr * b_diff
if i % 100 == 0:
print(f"Epoch {i}: 기울기 = {a:.4f}, 절편 = {b:.4f}")4) 그래프 확인
y_pred = a * x + b
plt.scatter(x, y) # 실제 데이터
plt.plot(x, y_pred, 'r') # 예측 선
plt.show()4. 경사 하강법을 활용한 학습 과정
경사 하강법은 다음과 같은 순서로 진행된다.
- 초기 값 설정: 기울기(a)와 절편(b)를 0으로 초기화
- 오차 계산: 예측 값과 실제 값의 차이를 계산
- 편미분 계산: MSE를 a와 b로 미분하여 기울기와 절편을 조정
- 업데이트 반복: 학습률을 적용해 값을 조정하며 최적화
- 최적 값 도출: 일정 반복 후 최적의 기울기와 절편을 찾음
최종적으로 a = 2.3, b = 79에 수렴하는 것을 확인할 수 있다. 이는 최소제곱법을 통해 계산한 결과와 동일하며, 경사 하강법을 통해서도 같은 결과를 얻을 수 있음을 보여준다.
5. 결론
경사 하강법은 데이터를 학습하여 점진적으로 최적의 기울기와 절편을 찾아가는 방법이다.
- 장점: 단순한 수학적 원리를 활용하여 모델을 최적화할 수 있다.
- 단점: 학습률 설정이 중요하며, 적절하지 않으면 최적 값에 수렴하지 않을 수 있다.
다중 선형 회귀(Multiple Linear Regression) 이해하기
머신러닝에서 회귀 분석은 입력 변수(독립 변수)와 결과 값(종속 변수) 사이의 관계를 찾는 중요한 방법이다. 단순 선형 회귀는 하나의 독립 변수와 하나의 종속 변수 간의 관계를 모델링하는 반면, 다중 선형 회귀는 여러 개의 독립 변수를 활용하여 하나의 종속 변수를 예측하는 기법이다.
1. 다중 선형 회귀란?
다중 선형 회귀는 독립 변수가 2개 이상인 경우에 적용하는 회귀 분석 방법이다. 수학적으로 다음과 같이 표현된다.
구성 요소
- y: 종속 변수(예측하려는 값)
- b0: 절편(intercept)
- b1, b2, ..., bn: 각 독립 변수에 대한 회귀 계수(기울기)
- x1, x2, ..., xn: 독립 변수(입력 변수)
- e: 오차(예측 값과 실제 값의 차이)
2. 다중 선형 회귀의 필요성
1) 현실 세계의 복잡한 데이터 설명
단순 선형 회귀는 하나의 변수만 고려하기 때문에 다양한 요소가 영향을 미치는 현실 데이터에는 적합하지 않다.
2) 변수 간 상호작용 반영
다중 선형 회귀는 여러 독립 변수가 종속 변수에 개별적으로 또는 동시에 영향을 미치는 관계를 모델링할 수 있다.
3) 더 정확한 예측 가능
여러 개의 변수를 활용하면 모델이 종속 변수를 더 정확하게 설명할 수 있다.
4) 통계적 분석과 의사 결정 지원
각 독립 변수의 기여도를 수치화하여 어떤 변수가 결과에 더 큰 영향을 미치는지 분석할 수 있다.
5) 다차원 데이터를 다룰 수 있음
2차원 이상의 데이터를 처리할 수 있어 고차원 문제에서도 유용하다.
3. 다중 선형 회귀 - 파이썬 코드 구현
중간고사를 본 4명의 학생의 공부한 시간(x1), 과외 수업 횟수(x2)와 성적(y) 데이터를 이용하여 다중 선형 회귀를 적용해보자.
1) 환경 및 데이터 준비
import numpy as np
import matplotlib.pyplot as plt
# 공부 시간(x1), 과외 수업 횟수(x2), 성적(y)
x1 = np.array([2, 4, 6, 8])
x2 = np.array([0, 4, 2, 3])
y = np.array([81, 93, 91, 97])2) 데이터 분포 확인 (3D 그래프 시각화)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter3D(x1, x2, y)
plt.xlabel("공부한 시간(x1)")
plt.ylabel("과외 수업 횟수(x2)")
ax.set_zlabel("성적(y)")
plt.show()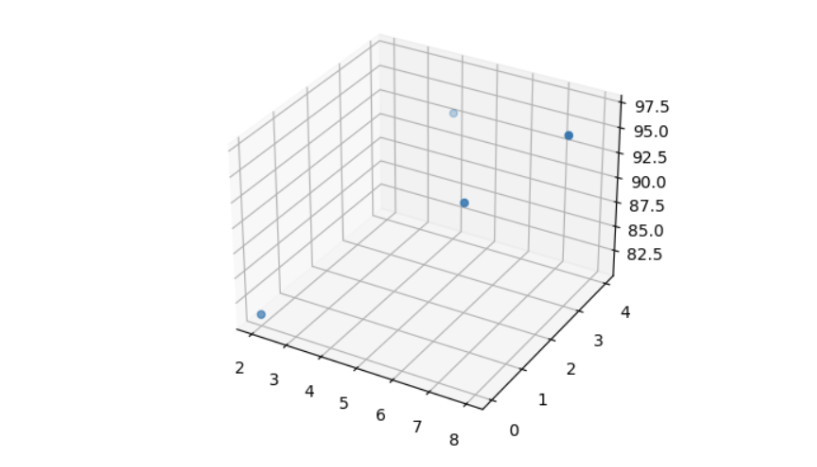
3) 실행을 위한 변수 설정
# 기울기 a1, a2와 절편 b 초기화
a1 = 0
a2 = 0
b = 0
# 학습률 설정
lr = 0.01
# 반복 횟수 설정
epochs = 20014) 경사 하강법 적용
n = len(x1) # 데이터 개수
for i in range(epochs):
y_pred = a1 * x1 + a2 * x2 + b # 예측 값 계산
error = y - y_pred # 오차 계산
# 오차 함수를 a1, a2, b에 대해 각각 편미분
a1_diff = -(2/n) * sum(x1 * error)
a2_diff = -(2/n) * sum(x2 * error)
b_diff = -(2/n) * sum(error)
# 학습률을 곱해 기울기와 절편 업데이트
a1 -= lr * a1_diff
a2 -= lr * a2_diff
b -= lr * b_diff
if i % 100 == 0:
print(f"epoch={i}, 기울기1={a1:.4f}, 기울기2={a2:.4f}, 절편={b:.4f}")5) 예측 결과 출력
print("실제 점수:", y)
print("예측 점수:", y_pred)4. 학습된 모델의 시각화 (3D 평면 그래프)
# 학습된 모델의 파라미터
a1_rst = 1.5
a2_rst = 2.2857
b_rst = 77.8569
ax = plt.axes(projection='3d')
# 3D 평면을 위한 x1, x2 좌표 생성
x1_range = np.linspace(min(x1), max(x1), 10)
x2_range = np.linspace(min(x2), max(x2), 10)
x1_grid, x2_grid = np.meshgrid(x1_range, x2_range)
y_pred = a1_rst * x1_grid + a2_rst * x2_grid + b_rst
# 3D 산점도 (실제 데이터)
ax.scatter(x1, x2, y, color='blue', label='Actual Data')
# 학습된 평면 시각화
ax.plot_surface(x1_grid, x2_grid, y_pred, color='orange', alpha=0.7, label='Prediction Plane')
ax.set_xlabel('study_hours(x1)')
ax.set_ylabel('private_class(x2)')
ax.set_zlabel('Score(y)')
ax.set_title('3D Linear Regression Visualization')
plt.show()5. 결론
다중 선형 회귀는 여러 개의 독립 변수를 이용하여 종속 변수를 예측하는 강력한 기법이다.
- 단순 선형 회귀보다 복잡한 데이터에 적합하며, 여러 변수가 동시에 영향을 미치는 경우 유용하다.
- 경사 하강법을 이용한 최적화를 통해 기울기와 절편을 점진적으로 조정하여 오차를 최소화할 수 있다.
- 3D 시각화를 통해 학습된 모델이 데이터와 어떻게 일치하는지 확인할 수 있다.
